Hexaflexagons are the ones first discovered and researched by the Flexagon Committee at Princeton University.  Several of the smaller faced versions of hexaflexagons are exibited on the home page.  On this page, I will dig a little deeper into hexaflexagons and present some templates for more advanced models.  These are all great fun to make and study.  Construction maps for hexaflexagons with less than 10 sides can be found on this link:  hexaflexagon construction maps .

DodecaHexaflexagon

12 Zodiac Faces with 4 Coded Variations

(Big file - 8MB!)

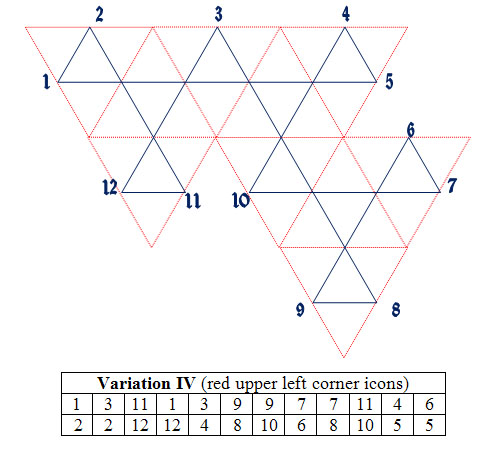
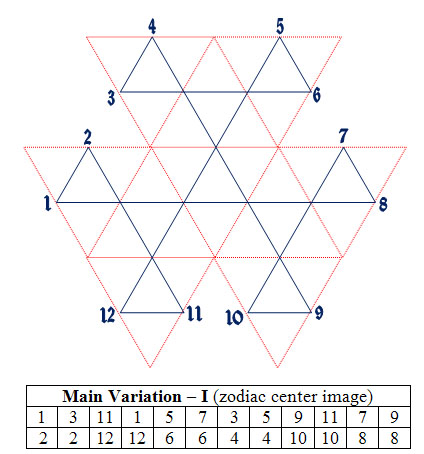
This flexagon is made from a straight strip of 36 triangles for a total of 72 triangle faces, twelve basic flexagon faces (with numerous triangle arrangements) for each of the 4 different folded variations.  I have coded this flexagon with 4 symbols on each triangle such that all four different foldings of the flexagon can be easily performed.  Each folding has a unique flexing traverse as well as unique sets of faces.  I have used  the 12 Zodiac months with 4 symbol sets for each Zodiac month to construct the faces of this flexagon.  See below for details of the construction and state diagrams for each of the four folded variations. Variations III and IV are mirror image patterns. I suggest making some of the simpler flexagons before constructing this one.  It will make it easier to recognize folding patterns and in flexing expectations.

DodecaHexaflexagon Construction Details

These diagrams do not include the Right and Left triangle orientations as would be necessary for designing most flexagons. Since this flexagon is a straight strip of triangles I left this detail out.  Note in each of the diagrams going from face to face the angle of the lines always changes, they are never parallel.  This is always the case for straight strip flexagons.  Note that variations III and IV are mirror images.  I have included a 5th variation not coded on the frieze below.  This variation is interestin as the Tuckerman diagram twists back on itself.  I have enlarged one of the triangles so that all the triangles can be seen.